Simple radiative balance model with atmospheric layer containing greenhouse gases

The Earth/atmosphere system as viewed from space must be in radiative equilibrium. The system receives radiation from the sun:

( 1)           S_oπR²

where S_o is the extraterrestrial constant (about 1360 W/m²) and R is the radius of the Earth/atmosphere system. The Earth/atmosphere system has a reflectivity (planetary albedo) of α = 0.29, so it reflects about 29% of the incoming radiation and absorbs the rest. The absorbed radiation must be balanced by thermal radiation from the Earth/atmosphere system according to the Stefan-Boltzmann law. Assuming the Earth/atmosphere system behaves like a perfect spherical blackbody radiator with an emissivity of 1 at T_e:

( 2)           πR²•S_o(1 – α) = 4πR²•σT_e⁴

Simplifying:

( 3)           (S_o/4)(1 – α) = σT_e⁴

Solve for the effestive radiating temperature of the Earth/atmosphere system as observed from space T_e:

( 4)           T_e = [(340•0.71)/5.67 x 10^-8) = 255.4 K ≈ –18°C

But, fortunately for life as we understand it, the average temperature at Earth's surface is about 15-16°C, a temperature which will support liquid water. The difference of about 34°C is a result of the greenhouse effect.

A useful extension of the radiative balance for the Earth/atmosphere system as viewed from space assumes a single-layer atmosphere at constant temperature (an isotropic atmosphere). The surface and atmosphere have different temperatures and presumably the effective temperature defined in ( 4) lies somewhere between these two values. Asssume that the atmosphere does not interact at all with incident and reflected (shortwave) solar radiation, but that it absorbs and re-radiates thermal radiation, equally downward and upward, acting like an imperfect blackbody with an emissivity ε less than 1. With this assumption, the Earth/atmosphere system albedo is the same as the average albedo of Earth's surface, including its average cloud cover; it is though clouds were "painted" onto Earth's surface rather than being part of and interacting with the atmosphere. This is not a bad assumption for a system in radiative balance.

At the top of the atmosphere the infrared flux F from the atmosphere to space is the flux emitted by the atmosphere itself at temperature T_a and the flux from Earth's surface at temperature T_s that escapes through the atmosphere:

( 5)           F↑ = εσT_a⁴ + (1 – ε)σT_s⁴

As viewed from space, this process still requires that the system be in radiative balance with the incoming radiation:

( 6)           (S_o/4)(1 – α) = εσT_a⁴ + (1 – ε)σT_s⁴

Energy balance at Earth's surface requires that the total incoming radiation, solar plus infrared flux emitted downward from the atmosphere, equals the outgoing thermal radiation:

( 7)           (S_o/4)(1 – α) + εσT_a⁴ = σT_s⁴

Eliminate (S_o/4)(1 – α) using (6) and (7):

( 8)           εσT_a⁴ + (1 – ε)σT_s⁴ = σT_s⁴ – εσT_a⁴

Solve for T_a:

( 9)           T_a = T_s/2^1/4 = 0.841•T_s

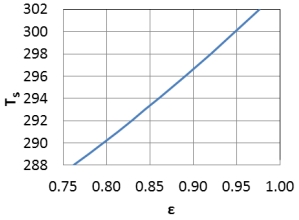
Figure 1. Surface temperature as a function of atmospheric emissivity.

Note that the relationship between T_a and T_s, the ratio of T_a to T_s, is independent of the assumed emissivity of the atmosphere.

Use the fact from ( 9) that T_a⁴ = T_s⁴/2, substitute in ( 7) to solve for T_s:

(10)           T_s = {[S_o(1 – α)/(4σ)][1/(1 – ε/2)]}^1/4

Note that (10) reduces to ( 3) and T_s = T_e if the atmosphere does not absorb and re-emit thermal radiation, that is, if there is no greenhouse effect.

From ( 3) and (10), T_s, and hence T_a, can be derived in terms of T_e:

(11)           T_s = T_e/(1 – ε/2)1/4

Through these equations, Earth's radiative balance is defined in terms of the planetary albedo α and the atmospheric emissivity ε. The solar constant determines the effective radiating temperature of the Earth/atmosphere system to space, and hence the values of T_a and T_s, but not the ratio of the two. What now?

We can use ε as an independent variable and calculate surface temperatures. Or, we can determine the average global surface temperature and use that value to determine the corresponding value of ε:

(12)           ε = 2[1 – S_o/(4σ)(1 – α)/T_s⁴)

If the global average surface temperature is 15°C, then ε has a value of 0.765. If it is 16°C, then ε is 0.782.

The single-layer isotropic atmosphere greenhouse model is summarized in Figure 2. The percentages are percentages of incoming solar radiation. The radiation incident on Earth's surface — a combination of absorbed incoming solar radiation and thermal radiation from the atmosphere — is balanced by thermal radiation leaving the surface. Radiation leaving the top of the atmosphere — a combination of reflected incoming solar radiation, thermal radiation from Earth's surface passing through the atmosphere, and thermal radiation from the atmosphere — is equal to the total incoming solar radiation. For a system in equilibrium, the incoming and outgoing radiation must continue to balance both at Earth's surface and the top of the atmosphere. How the balance is achieved depends on the planetary albedo, which can be changed by changing average cloudiness, for example, and the emissivity of the atmosphere, which can be changed by changing concentrations of greenhouse gases (including water vapor). Changing these values will change temperatures at the surface and in the atmosphere. Temperatures can also be changed by changing the extraterrestrial constant. This simple model "decouples" Earth's surface and its atmosphere, which is not true in the real world in which solar/atmosphere/surface processes are interconnected in multiple and complex ways. But, it provides a conceptual starting point for thinking about interactions between surface and atmosphere and the physical processes that might modify both the planetary albedo (including the effects of cloud cover) and the behavior of the atmosphere. Ultimately, the "big questions" of climate lie with determining how natural processes and anthropogenic activities modify albedo and atmospheric emissivity.		Figure 2. Simple greenhouse model with single-layer isotropic atmosphere.

The single-layer atmosphere model can be extended to multiple layers, with each layer having its own emissivity. In such a model, it would also be necessary to consider that the atmosphere, as a whole, is not completely transparent to incoming solar radiation. For example, there are several large water vapor absorption bands that influence the amount of solar radiation reaching Earth's surface. Thus, a multi-layer atmosphere approach requires a much more detailed understanding of atmospheric properties.